* 이 포스트는 Coursera에 있는 Andrew Ng 교수님의 강의 Machine Learning(링크)를 바탕으로 작성되었습니다.

Gradient Descent

저번 포스팅에서 언급했던 Cost Function의 최소값을 다시 한 번 생각해보자.

다음은 θ₀을 x축, θ₁을 y축, J(θ₀, θ₁)을 z축으로 하는 그래프의 예이다.

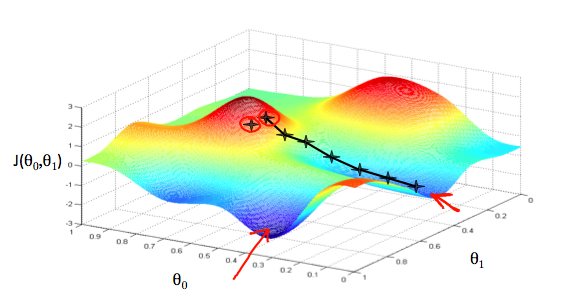
이 그래프에서 가장 아래있는 점의 x, y 좌표 즉 θ₀와, θ₁을 알아내는 것이 좋은 hypothesis function 만들기의 목표이다.

이 최소값은 cost function의 미분을 통해서 구할 수 있는데, 어떤 점에서 미분을 해서 나온 기울기 값이 최소값으로 향하는 방향을 제시한다는 것이다.

이런 방법으로 θ를 구하는 게 gradient descent 의 algorithm이다.

한편 이렇게 미분을 통해 나온 기울기 값으로 점점 최소값으로 향할 때 얼마만큼 이동할지는 learning rate인 상수값으로 설정하는데 보통 learning rate는 α라고 쓴다.

learning rate 이야기는 잠시 후에 하고 일단 이렇게 cost function의 최소값을 구하는 gradient descent의 algorithm을 살펴보자.

위의 알고리즘은 각 θ에 cost function을 편미분한 값에 α를 곱한만큼 반복해서 뺀다.

여기서 중요한 부분은 각 θ에 대해 simultaneous update를 해줘야한다는 점이다.

위를 보면 simultaneous update와 그렇지 않은 update의 차이를 알 수 있을 것이다.

이제 learning rate를 어떻게 설정해야 하는지 생각해보자.

learning rate가 작으면 θ 값이 작게 변하므로 cost function의 최소값에 가는데 오래 걸릴 것이고,

learning rate가 클수록 θ 값이 크게 변하므로 cost function의 최소값에 금방 도달할 수 있을 것이다.

하지만 learning rate가 어느 정도 이상으로 커지면 다음과 같은 문제가 발생한다.

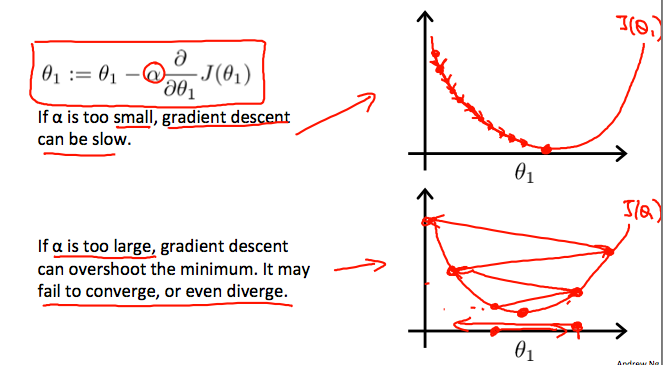
learning rate가 너무 커지면 위와 같이 최소값에 도달 하지 않을 수도 있다는 것이다.

따라서 적당한 learning rate를 설정해야하는데, 이건 data set마다 변화하는 정도가 다르므로 거기에 맞게 정해줘야한다.

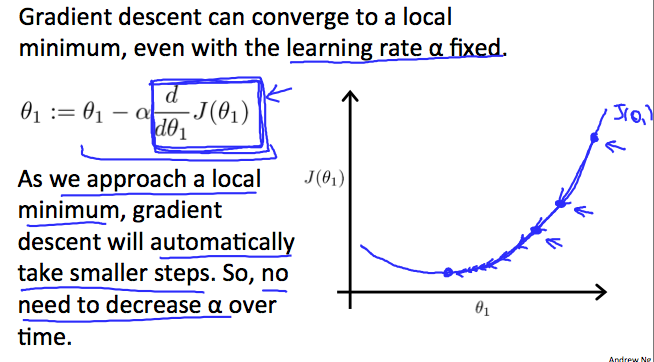
또한 위에서 learning rate는 상수라고 했었는데 최소값에 더 정밀하게 다가가기 위해서 변수로 지정하지 않아도 괜찮다.

왜냐하면 최소값에 가까워질수록 각각 점에서의 기울기가 감소하므로 천천히 최소값에 접근하기 때문이다.

learning rate에 대해서는 다음 포스팅에서도 이야기를 할 것이다.

사실 위에서 보여준 예시는 다 Linear Regression이긴 한데, 눈으로 보여주기가 용이해서 예시를 든 것이지 다른 hypothesis function에도 똑같이 적용이 된다.

Gradient Descent For Linear Regression

이제 Linear Regression의 Gradient Descent에 대해서 집중적으로 생각해보자.

traning set이 1개라고 했을 때, Cost function을 편미분한 값은 다음과 같다.

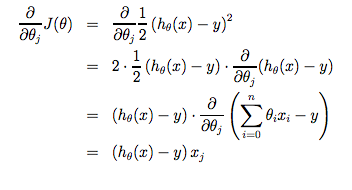
여기서 x₀, x₁은 편의상 h(x) = θ₀ + θ₁x = θ₀x₀ + θ₁x₁으로 표기했으며, x₀ = 1이다.

이를 Gradient Descent algorithm에 적용하면,

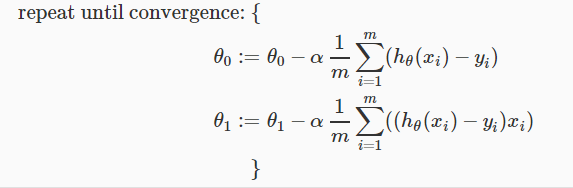
이렇게 나오는데 이 algorithm대로 θ를 구하면 된다.

그런데 Gradient Descent는 local optimum을 구하는 algorithm이다.

하지만 local optimum은 가장 좋은 θ가 아니라 global optimum일때 cost function이 최소가 되므로 그 때의 θ가 가장 적합하다.

그래서 Gradient Descent는 convex한 cost function에서만 해를 구할 수 있다.

Linear Regression에서 cost function은 quadratic 하므로 local optimum이 global optimum이고 Gradient Descent를 이용하면 최적의 hypothesis function을 만들 수 있다.

다음 포스팅에서는 Multivariate Linear Regression에 대해서 알아보겠다.