* 이 포스트는 Coursera에 있는 Andrew Ng 교수님의 강의 Machine Learning(링크)를 바탕으로 작성되었습니다.

Multiple Feature

Data set의 feature가 여러 개인 경우의 Linear Regression을 Multivariate Linear Regression이라고 한다.

집 값 예측하기에 빗대어 설명하면 집의 크기 외에도 마당의 크기, 편의시설과 가까운 정도 등 다른 요인까지 생각했다고 보면 된다.(h(x)가 linear 하다고 했을 때.)

앞으로 나올 용어 정리를 하자면 x_j⁽ⁱ⁾ = i번째 training example의 j번째 feature 값 이고,

h(x)는 다음과 같다.

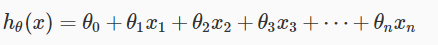
feature가 n개 이지만 vectorization을 위해 θ₀ = θ₀x₀, 즉 x₀ = 1 이라 하면 h(x)는 이렇게도 표현이 가능하다.

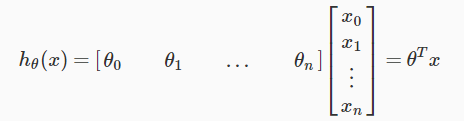
이제 행렬 연산으로 h(x)를 간편하게 계산할 수 있게 되었다.

Gradient Descent For Multiple Variables

multiple variables 일때도 gradient descent 방정식은 형태가 같다.

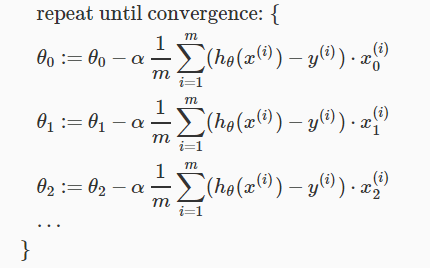
즉,

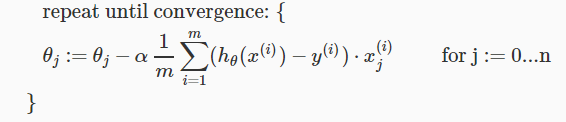
이다.

다음은 feature 가 1개 일 때와 여러 개 일때 gradient descent algorithm을 비교한 것이다.

Feature Scaling

input value의 범위를 일치시키면 좀 더 빨리 gradient descent를 구할 수 있다.

input value가 고르지 못할 때, 작은 범위에서는 θ가 천천히 변하고 큰 범위에서는 θ가 빨리 변하게 되므로 비효율적으로 진동하게 되기 때문이다.

보통 정규화를 시켜서 늘리거나 줄이는데, 범위만 일치시키면 크게 문제는 없다.

-1 ≤ x_i ≤ 1 이나 -0.5 ≤ x_i ≤ 0.5 등 이렇게 설정해도 상관은 없는데 모든 변수에만 똑같이 적용시키면 된다는 뜻이다.

보통은 다음과 같이 정규화시킨다.

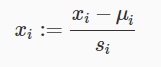
여기서 μ_i은 해당 i번째 feature의 평균값이고, s_i는 해당 i번째 feature 중에서 최대값과 최소값을 뺀 만큼의 값이다.

예를 들어서 price라는 feature가 100~2000 사이의 값을 가지고 있고 평균값이 1000이라면,

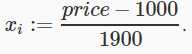
이다.

Learning Rate

gradient descent를 이용해서 θ를 구할 때, Cost function 즉 J(θ)가 매 반복마다 줄어야한다.

보통 gradient descent에서 J(θ)가 iteration 한 번에 아주 작은 값(ex. 10^-3) 보다 적게 줄어들면 수렴한다고 판단한다.

그런데 반복할 때 마다 J(θ)가 줄어들거나 수렴하지 않고 증가한다면 문제는 learning rate에 있다.

J(θ)가 너무 천천히 줄어드는 것 또한 learning rate 설정의 오류이다.

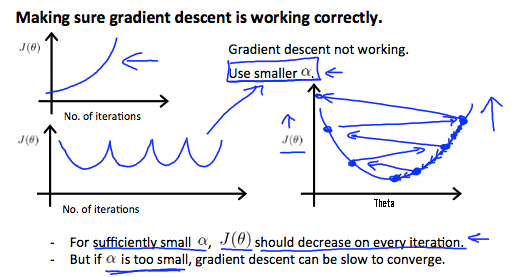
요약하자면,

α가 너무 작다: 수렴하는 값을 찾는게 오래걸린다.
α가 너무 크다: 매 반복마다 감소하지 않고 수렴하지 않는다.

Features and Polynomial Regression

주어진 data의 feature를 잘 분석하면 성능 향상에 도움이 되는데, 여러 개의 feature를 조합해 하나로 만들 수도 있다.

예를 들면, 집 값을 예측하기 위해 집의 frontage(x₁), depth(x₂)라는 feature가 있다고 했을 때 이 두 개를 곱한 area(x₃=x₁x₂)라는 새로운 feature를 만들 수 있다는 말이다.

또한 Data set의 분포를 보고 그에 적합한 hypothsis function을 설정할 수 있는데, linear 뿐만 아니라 quadratic, cubic 또는 square root의 hypothesis function도 가능하다.

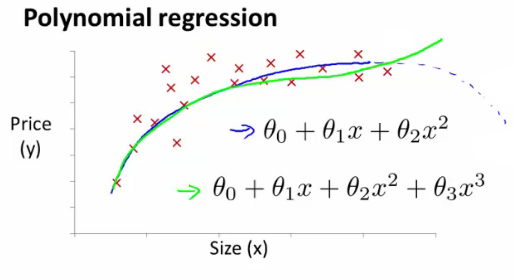
위의 그래프에서 size라는 feature를 가지고 hypothesis function을 설정하면 cubic한 다항식이 될 것이다.

이때 θ₃x³에서 x를 세제곱을 했기 때문에 다른 항에 비해서 x값의 증가량에 비해 변화량이 크므로 feature scaling에 유의해야한다.