Coursera 강의 “Machine Learning with TensorFlow on Google Cloud Platform” 중 다섯 번째 코스인 Art and Science of Machine Learning의 강의노트입니다.


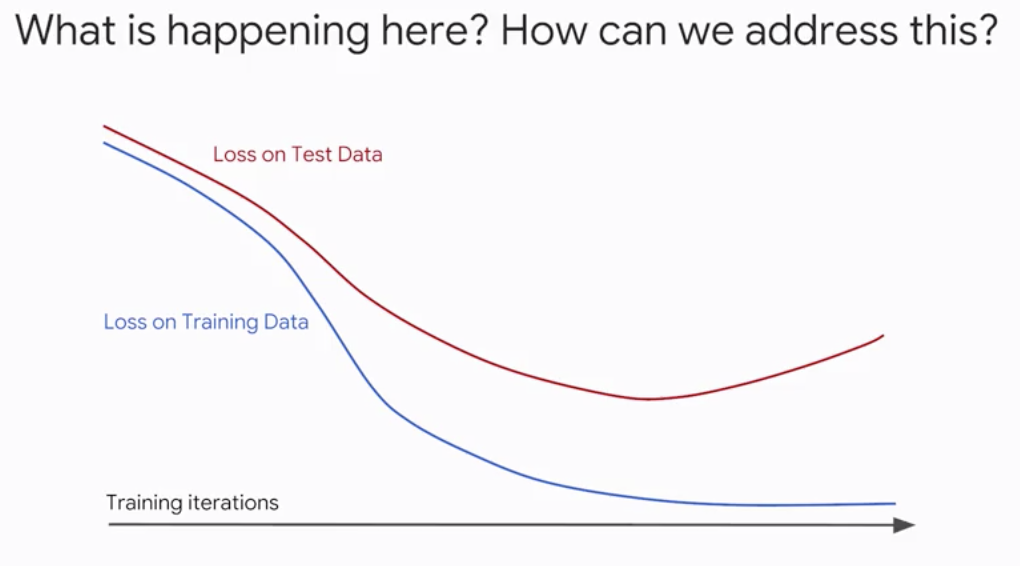
Regularization


  • The simpler the better

  • Factor in model complexity when calculating error

    • Minimize: loss(Data|Model) + complexity(Model)
    • loss is aimed for low training error
    • but balance against complexity

    • Optimal model complexity is data-dependent, so requires hyperparameter tuning Regularization is a major field of ML research

    • Early Stopping
    • Parameter Norm Penalties
      • L1 / L2 regularization
      • Max-norm regularization
    • Dataset Augmentation
    • Noise Robustness
    • Sparse Representations
    • …


L1 & L2 Regularizations

  • How can we measure model complexity?

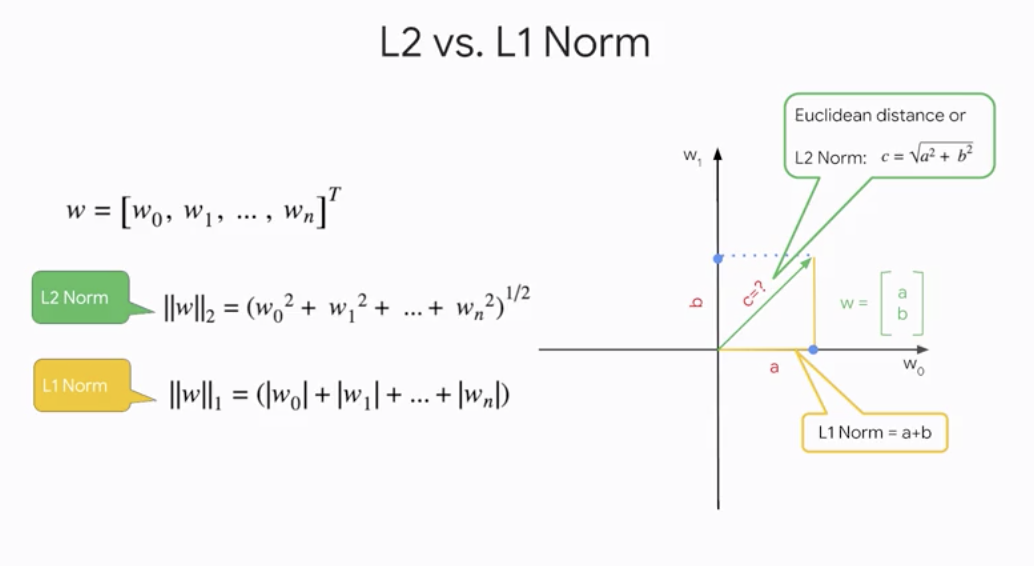
L2 vs. L1 Norm
L2 vs. L1 Norm

  • In L2 regularization, complexity of model is defined by the L2 norm of the weight vector

    \[L(w,D)+\lambda||w||_{\color{Red}2}\]
    • lambda controls how these are balanced

  • In L1 regularization, complexity of model is defined by the L1 norm of the weight vector

    \[L(w,D)+\lambda||w||_{\color{Red}1}\]
    • L1 regularization can be used as a feature selection mechanism

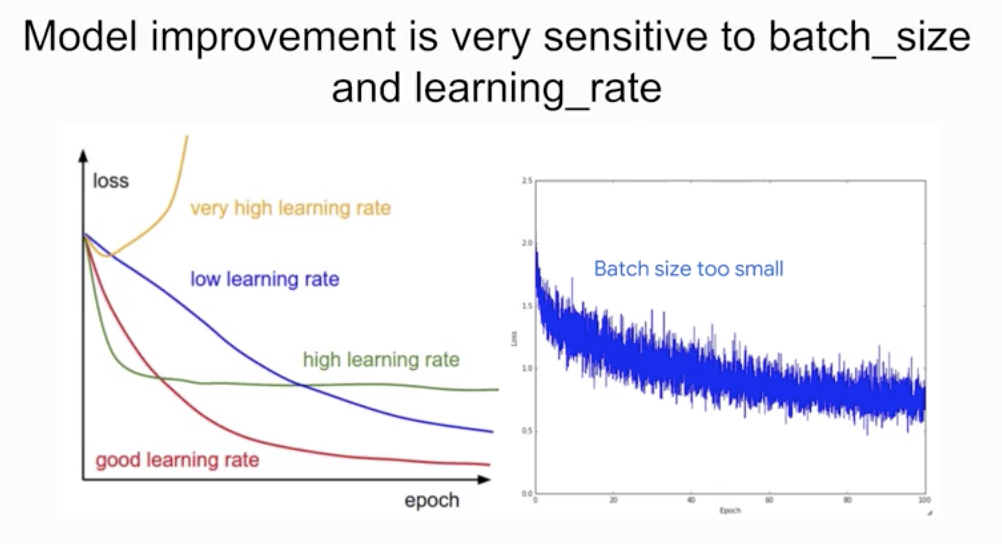
Learning rate and batch size

  • We have several knobs that are dataset-dependent
  • Learning rate controls the size of the step in weight space
    • If too small, training will take a long time
    • If too large, training will bounce around
    • Default learning rate in Estimator’s LinearRegressor is smaller of 0.2 or 1/sqrt(num_features) → this assume that your feature and label values are small numbers
  • The batch size controls the number of samples that gradient is calculated on
    • If too small, training will bounce around
    • If too large, training will take a very long time
    • 40 - 100 tends to be a good range for batch size Can go up to as high as 500
  • Regularization provides a way to define model complexity based on the values of the weights


Optimization

  • Optimization is a major field of ML research
    • GradientDescent — The traditional approach, typically implemented stochastically i.e. with batches
    • Momentum — Reduces learning rate when gradient values are small
    • AdaGrad — Give frequently occurring features low learning rates
    • AdaDelta — Improves AdaGrad by avoiding reducing LR to zero
    • Adam — AdaGrad with a bunch of fixes
    • Ttrl — “Follow the regularized leader”, works well on wide models
    • …
    • Last two things are good defaults for DNN and Linear models


Practicing with TensorFlow code

  • How to change optimizer, learning rate, batch size
 
train_fn = tf.estimator.inputs.pandas_input_fn(..., batch_size=10)
myopt = train.FtrlOptimizer(learning_rate=0.01,
​							l2_regularization_strength=0.1)
model = tf.estimator.LinearRegressor(..., optimizer=myopt)
model.train(input_fn=train_fn, steps=10000)
  1. Control batch size via the input function
  2. Control learning rate via the optimizer passed into model
  3. Set up regularization in the optimizer
  4. Adjust number of steps based on batch_size, learning_rate
  5. Set number of steps. not number of epochs because distributed training doesn’t play nicely with epochs.


Hyperparameter Tuning

  • ML models are mathematical functions with parameters and hyper-parameters
    • Parameters changed during model training
    • Hyper-parameters set before training
  • Model improvement is very sensitive to batch_size and learning_rate


  • There are a variety of model parameters too
    • Size of model
    • Number of hash buckets
    • Embedding size
    • Etc.
    • Wouldn’t it be nice to have the NN training loop do meta-training across all these parameters?
  • How to use Cloud ML Engine for hyperparameter tuning
    1. Make the parameter a command-line argument
    2. Make sure outputs don’t clobber each other
    3. Supply hyperparameters to training job


Regularization for sparsity

  • Zeroing out coefficients can help with performance, especially with large models and sparse inputs

    • Fewer coefficients to store / load → Reduce memory, model size
    • Fewer multiplications needed → Increase prediction speed
    \[L(w, D)+\lambda\sum^n|w|\]
    • L2 regularization only makes weights small, not zero

  • Feature crosses lead to lots of input nodes, so having zero weights is especially important

  • L0-norm(the count of non-zero weights) is an NP-hard, non-convex optimization problem

  • L1 norm(sum of absolute values of the weights) is convex and efficient; it tends to encourage sparsity in the model

  • There are many possible choices of norms


  • Elastic nets combine the feature selection of L1 regularization with the generalizability of L2 regularization

    \[L(w,D)+\lambda_1\sum^n|w|+\lambda_2\sum^nw^2\]


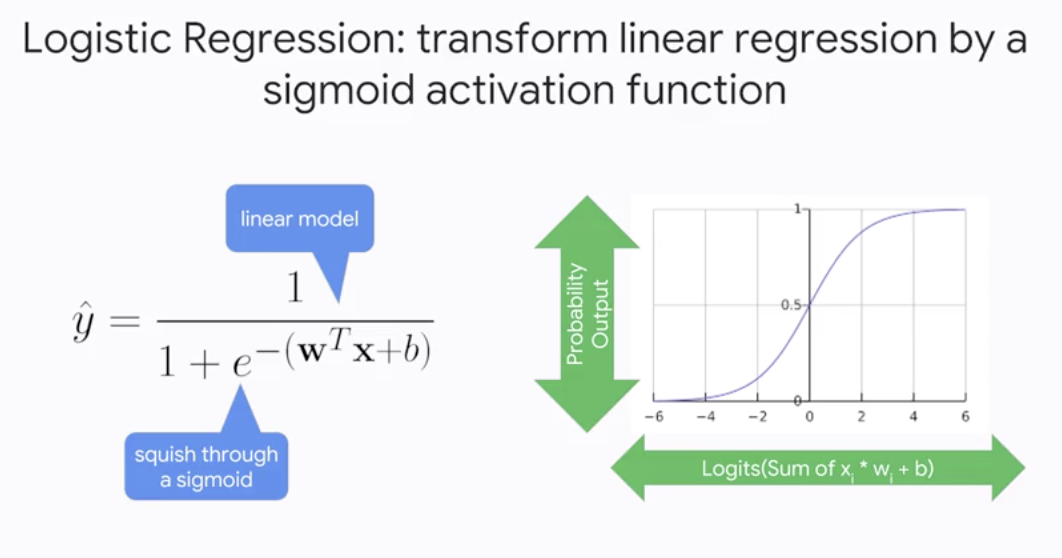
Logistic Regression

  • Transform linear regression by a sigmoid activation function

Logistic Regression
Logistic Regression

  • The output of Logistic Regression is a calibrated probability estimate

    • Useful because we can cast binary classification problems into probabilistic problems: Will customer buy item? becomes Predict the probability that customer buys item

  • Typically, use cross-entropy (related to Shannon’n information theory) as the error metric

    • Less emphasis on errors where the output is relatively close to the label.
    \[LogLoss = \sum_{(x,y)\in D}-ylog(\hat{y})-(1-y)log(1-\hat{y})\]

  • Regularization is important in logistic regression because driving the loss to zero is difficult and dangerous

    • Weights will be driven to -inf and +inf the longer we train
    • Near the asymptotes, gradient is really small

  • Often we do both regularization and early stopping to counteract overfitting


  • In many real-world problems, the probability is not enough; we need to make a binary decision
    • Choice of threshold is important and can be tuned
  • Use the ROC curve to choose the decision threshold based on decision criteria


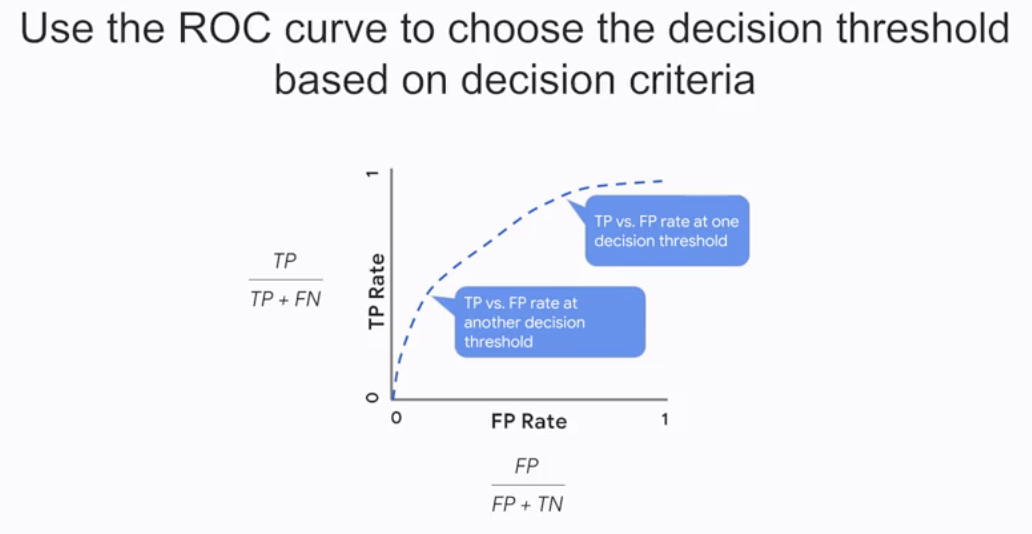
  • The Area-Under-Curve(AUC) provides an aggregate measure of performance across all possible classification thresholds
    • AUC helps you choose between models when you don’t know what decision threshold is going to be ultimately used.
    • “If we pick a random positive and a random negative, what’s the probability my model scores them in the correct relative order?”
  • Logistic Regression predictions should be unbiased
    • average of predictions == average of observations
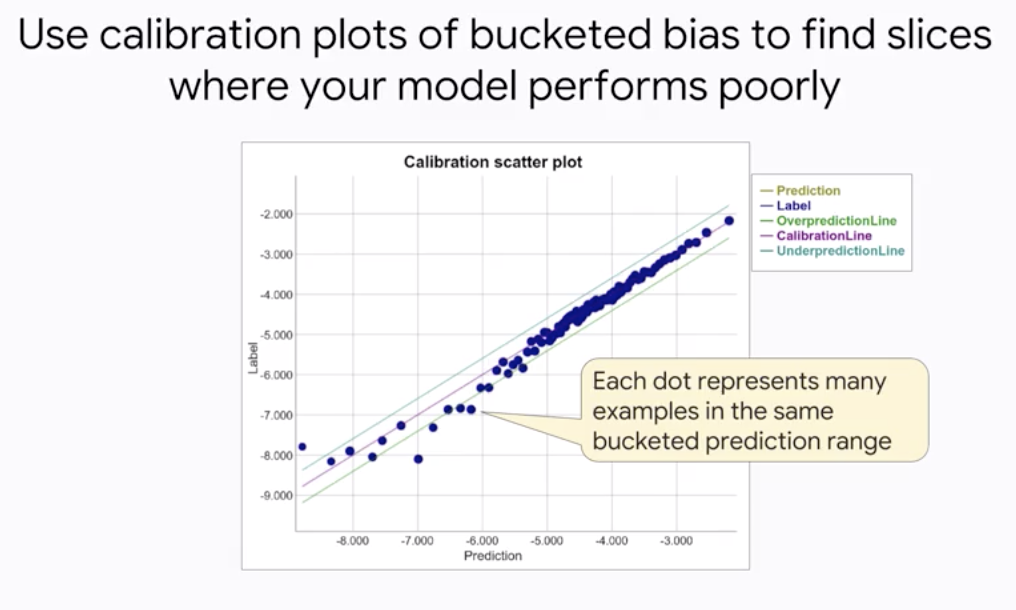
    • Look for bias in slices of data. this can guide improvements
  • Use calibration plots of bucketed bias to find slices where your model performs poorly



Neural Networks

  • Feature crosses help linear models work in nonlinear problems
    • But there tends to be a limit…
  • Combine features as an alternative to feature crossing
    • Structure the model so that features are combined Then the combinations may be combined
    • How to choose the combinations? Get the model to learn them
  • A Linear Model can be represented as nodes and edges
  • Adding a Non-Linearity



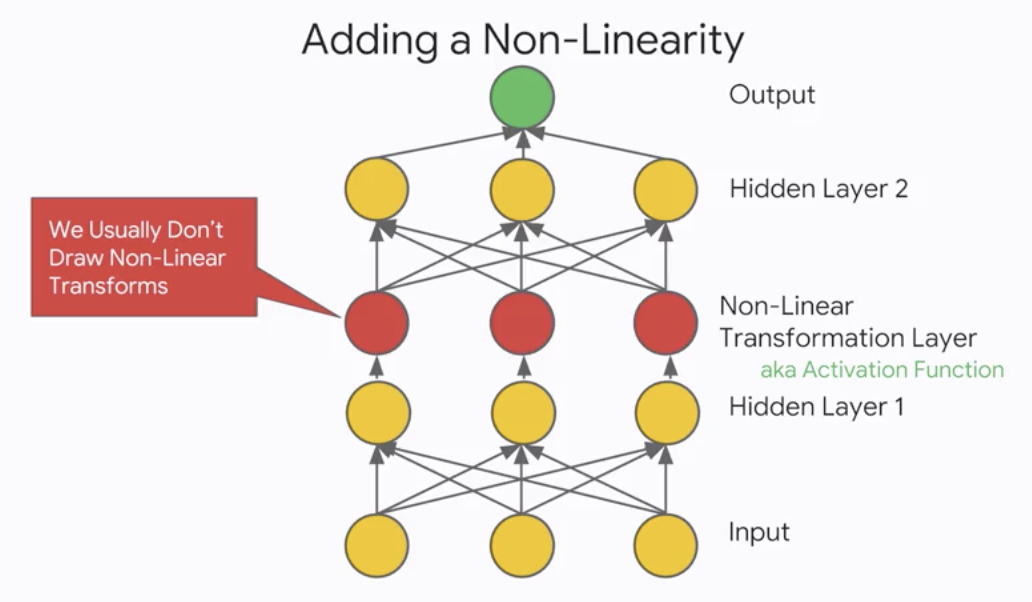
  • Our favorite non-linearity is the Rectified Linear Unit (ReLU)
\[f(x) = max(0,x)\]

  • There are many different ReLU variants

    \[Softplus = ln(1+e^x)\] \[Leaky ReLU=f(x)=\begin{cases}0.01x&for&x>0\\x&for&x\le0\end{cases}\] \[PReLU=f(x)=\begin{cases}\alpha x&for&x>0\\x&for&x\le0\end{cases}\] \[ReLU6=min(max(0,x),6)\] \[ELU=f(x)=\begin{cases}\alpha (e^x-1)&for&x>0\\x&for&x\le0\end{cases}\]

  • Neural Nets can be arbitrarily complex

    • Hidden layer - Training done via BackProp algorithm: gradient descent in very non-convex space
    • To increase hidden dimension, I can add neurons
    • To increase function composition, I can add layers
    • To increase multiple labels per example, I can add outputs


Training Neural Networks

  • DNNRegressor usage is similar to LinearRegressor
 
myopt = tf.train.AdamOptimizer(learning_rate=0.01)

model = tf.estimator.DNNRegressor(model_dir=outdir,
​					hidden_units=[100, 50, 20],
​					feature_colimns=INPUT_COLS,
​					optimizer=myopt,
​					dropout=0.1)

NSTEPS = (100 * len(traindf)) / BATCH_SIZE
model.train(input_fn=train_input_fn, steps=NSTEPS)
  • Use momentum-based optimizers e.g. Adagrad(the default) or Adam.
  • Specify number of hidden nodes.
  • Optionally, can also regularize using dropout
  • Three common failure modes for gradient descent


  • There are benefits if feature values are small numbers
    • Roughly zero-centered, [-1, 1] range often works well
    • Small magnitudes help gradient descent converge and avoid NaN trop
    • Avoiding outlier values helps with generalization
  • We can use standard methods to make feature values scale to small numbers
    • Linear scaling
    • Hard cap (clipping) to max, min
    • Log scaling
  • Dropout layers are a form of regularization


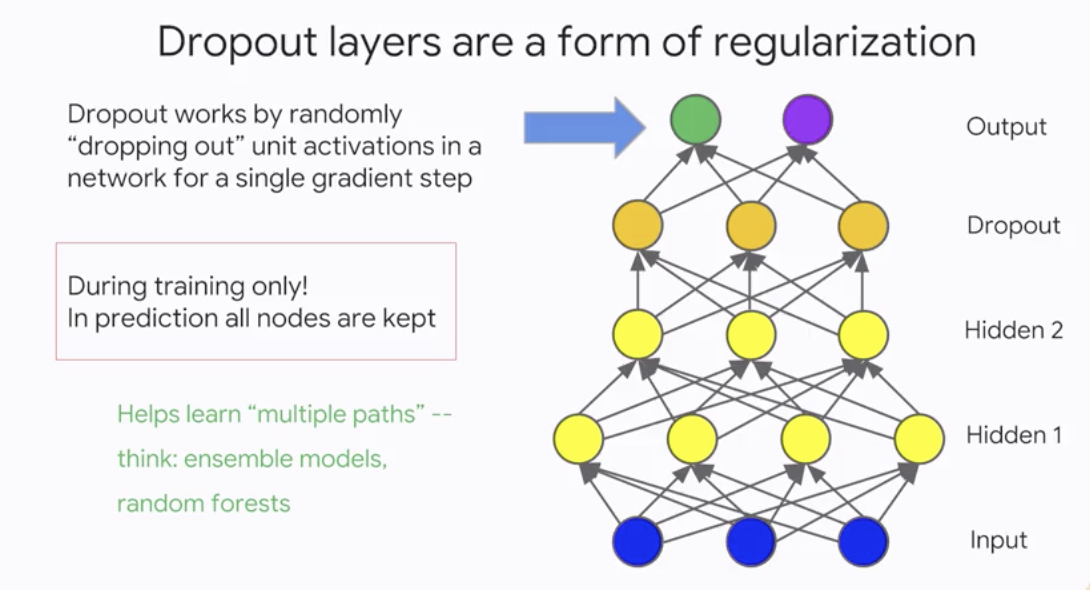
  • Dropout simulates ensemble learning
  • Typical values for dropout are between 20 to 50 percent
  • The more drop out, the stronger the regularization
    • 0.0 = no dropout regularization
    • Intermediate values more useful, a value of dropout=0.2 is typical
    • 1.0 = drop everything out! learns nothing
  • Dropout acts as another form of Regularization. It forces data to flow down multiple paths so that there is a more even spread. It also simulates ensemble learning. Don’t forget to scale the dropout activations by the inverse of the keep probability. We remove dropout during inference.


Multi-class Neural Networks

  • Logistic regression provides useful probabilities for binary-class problems
  • There are lots of multi-class problems
    • How do we extend the logits idea to multi-class classifiers?
  • Idea: Use separate output nodes for each possible class
  • Add additional constraint, that total outputs = 1.0


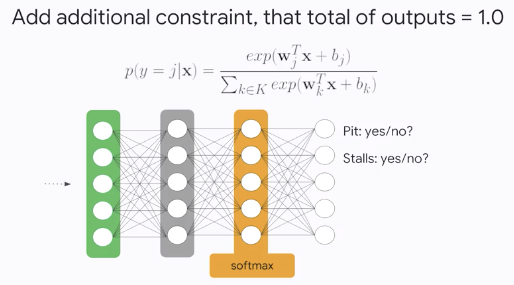
  • Use one softmax loss for all possible classes
 
logits = tf.matmul(...) # logits for each output node -> shape=[batch_size, num_classes]
labels =                # one-hot encoding in [0, num_class] -> shape=[batch_size, num_classes]
loss = tf.reduce_mean(
​			tf.nn.softmax_cross_entropy_with_logits_v2(
​				logits, labels) # shape=[batch_size]
}
  • Use sotfmax only when classes are mutually exclusive
    • “Multi-Class, Single_label Classification”
    • An example may be a member of only one class.
    • Are there multi-class setting where examples may belong to more than one class?
 
tf.nn.sigmoid_cross_entropy_with_logits(logits, labels) # shape=[batch_size, num_classes]
  • If you have hundreds or thousands of classes, loss computation can become a significant bottleneck
    • Need to evaluate every output node for every example
  • Approximate versions of softmax exist
    • Candidate Sampling calculates for all the positive labels, but only for a random sample of negatives: tf.nn.sampled_softmax_loss
    • Noise-contrastive approximates the denominator of softmax by modeling the distribution of outputs: tf.nn.nce_loss
  • For our classification output, if we have both mutually exclusive labels and probabilities, we should use tf.nn.softmax_cross_entropy_with_logits_v2.
  • If the labels are mutually exclusive, but the probabilities aren’t, we should use tf.nn.sparse_softmax_cross_entropy_with_logits.
  • If our labels aren’t mutually exclusive, we should use tf.nn.sigmoid_cross_entropy_with_logits.