* 이 포스트는 Coursera에 있는 Andrew Ng 교수님의 강의 Machine Learning(링크)를 바탕으로 작성되었습니다.

Classification

지금까지 공부해본 regression과 달리 classification에서는 discrete value를 다룬다.

제일 간단한 방법은 모든 data 값을 0과 1 사이에 mapping 시키고 그 값이 0.5를 기준으로 작으면 0, 크면 1 이라고 예측하는 것이다.

하지만 모든 케이스가 linear한 형태를 띄고 있지는 않으므로 이 방법보단 기준 값을 두어 일정 값 이상이면 1 이라고 예측하는 방법을 주로 사용한다.

한편, 위에서도 언급했던 것 처럼 classification 문제는 예측할 값이 discrete value라는 걸 빼면 regression 과 비슷하다.

일단 예측 결과 값 y가 두 가지 값(0, 1; 각 케이스rable을 만든다) 밖에 가질 수 없는 binary classification에 대해서 생각해보자.(여기서 multiple classification으로도 일반화 시킬 수 있다.)

예를 들면,

· 환자의 종양이 악성인지(0 또는 1) / 아닌지(1 또는 0)
· 메일이 스팸인지(0 또는 1) / 아닌지(1 또는 0)

등이 있다.

Hypothesis Representation

Classification은 data값을 0과 1사이에 mapping 시켜 이루어진다고 했는데, 이렇게 mapping 시키는 함수를 hypothesis function이라 한다.

하지만 모든 데이터의 값에 비례해 linear regression과 같은 방식으로 hypothesis function을 만들면 좋은 예측을 할 수 없다.

이를 해결하기 위해 Logistic Function, 혹은 Sigmoid Function 이라는 함수를 이용하는데, 이는 다음과 같다.

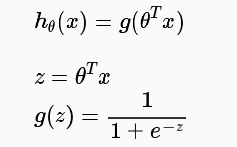
이러한 sigmoid function의 그래프는 아래와 같다.

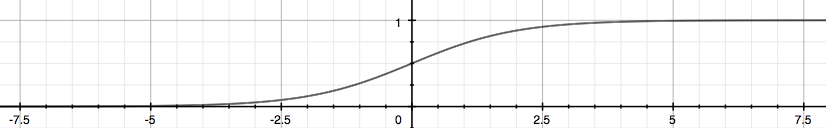
이 함수 g(z)는 결과가 1이 나올 확률을 나타낸다.

예를 들면, 위 함수에서 g(z) = 0.7 일 때 y = 1일 확률이 70 %가 된다는 것이다.

또한 결과가 1이 나올 확률과 0이 나올 확률의 합은 항상 1이므로 결과에 따른 확률도 다음과 같이 표현 가능하다.

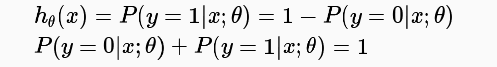
Decison Boundary

위의 과정을 통해 0 또는 1로 classification 하기 위해서, hypothesis function의 결과값을 다음으로 나타낼 수 있다.

logistic function을 생각해보면 결국 다음과 같다는 것도 알 수 있을 것이다.

이렇게 결과 값을 0 또는 1로 구별하는 지점을 decision boundary라고 하는데, 다음의 예를 살펴보자.

다음과 같은 두 class가 있을때, 이 class를 구분하는 decision boundary를 찾기 위해 hypothesis function h(x) = g(θ₀ + θ₁x₁ + θ₂x₂)를 만들어 보자.

이때 θ = {-3, 1, 1}로 잡으면 x로 표시된 부분은 y = 1이 될 것이고, o로 표시된 부분은 y = 0이 될 것이다.

이렇게 g(z) = 0, 즉 h(x) = 0.5를 만족시키는 부분을 Decision boundary 라고 한다.